• 
• 
• 
• 
• 
• 
• Pt. 1 of 4

Introduction

Bell’s inequality violations and Wheeler’s delayed-choice experiments have both been interpreted as implying that the choice of measurement, i.e., the experimenter’s decision on how to configure a detector, can alter the quantum mechanical state of a system that is spatially separated (in the relativistic sense[1]) from the event of making a choice. If altering the quantum mechanical state (as described by the wave function) constitutes a real physical change, we would have an apparently strong violation of the relativistic account of spacetime, which forbids signal transmission, much less real causal efficacy, between spacelike separated events. Permitting such a violation seems to imply, more radically, that the present can affect what is past (at least in some frames of reference), resulting in causal paradoxes. Attempts to face these implications range from denying the principle of causality to questioning whether the quantum mechanical state is a true image of physical reality. Discussions of these issues by physicists have been uneven in quality, often conflating the distinct principles of causality, reality, determinism, and locality. Here we hope to provide a systematic (though by no means exhaustive) exposition of these issues with sufficient rigor to satisfy physicists and philosophers, while keeping the basic concepts intelligible to non-physicists and non-mathematicians.

We will begin with a discussion for non-physicists of the quantum mechanical description of states and the notion of entangled states. This will facilitate understanding of the problem presented by Einstein, Podolsky and Rosen (EPR) in 1935,[2] where the choice of which property to measure in one system could alter the wave function of some spatially separated system. Operating on the assumption that it is impossible for the choice-of-measurement event to affect the physical reality of a spatially separated non-interacting system (Einstein’s relativistic principle of locality), it seemed to follow that the quantum wave function cannot be a complete account of physical reality. We will examine the argument by Einstein et al. in some detail, as it has often been characterized as positing local realism, when in fact it surreptitiously incorporates determinism into its definition of physical reality. Following our discussion of the EPR paper, we will take care to define terms such as ‘determinism’ and ‘realism’ in a way that facilitates conceptual clarity.

At the end of their paper, EPR suggested that it was possible, at least in principle, to complement the merely statistical description of physical reality provided by quantum mechanics with a complete description of physical reality. This hypothetical complement came to be known as hidden variables, i.e., variables in addition to those contained in the quantum wave function.

Remarkably, J.S. Bell in 1964 proved mathematically that this hidden variables hypothesis was testable,[3] using a thought experiment where the statistical distribution of outcomes predicted by quantum mechanics was different from that implied by the existence of any hidden variables that fully determine the physical reality of each member of the entangled pair prior to choice of measurement. The violation of a certain inequality in the probability of outcomes would absolutely preclude any hidden variables solution. It was no longer possible to appeal to our ignorance or incomplete knowledge of physical reality. Violation of a Bell’s inequality would prove with mathematical certainty (or at least to the degree of statistical certainty provided by actual experiments) that all hidden variables solutions (at least those obeying a principle of locality) were simply wrong. We will discuss the version of Bell’s thought experiment discussed by J.J. Sakurai (1994),[4] to make clear how strong the proof is, and why the attempts by some philosophers to make appeals to ignorance or imperfect knowledge are misguided.

Bell’s inequality violations were confirmed in a variety of experiments in the late twentieth century, though, as Bohm & Hiley (1993) noted, there was yet no strict proof that the two observation points were in fact spatially separated, due to insufficient accuracy in the timing of measurements.[5] This loophole was closed by Weihs et al. (1998).[6]

The common interpretation of these results by physicists is that local determinism is impossible. (Many have also inferred incorrectly that local realism is impossible, due to the conflation of realism and determinism by EPR.) This leaves three logical alternatives: local non-determinism, non-local determinism, and non-local determinism. Initially, most physicists adopted the first option, preferring to accept randomness as a fundamental reality rather than contradict relativity by non-locality. By the 1990s, however, non-local interpretations were openly held by many mainstream physicists, even those who were not trying to save determinism. Alternative ontological interpretations of quantum mechanics have generally accepted Bell’s dilemma, either preserving determinism and accepting non-locality (Bohm), or preserving locality while accepting non-determinism (Griffiths’ consistent histories).

Notably, Gerard ’t Hooft (2007) has challenged the premise that a violation of Bell’s inequality disproves local determinism.[7] He has argued that this common interpretation relies on a notion of free will that is incompatible with the hypothesis of determinism ostensibly being tested. Instead, he considers that the wave function characterizing states and the operators characterizing observable properties are interdependent in their time evolution, so that there is no more paradox in a choice of measurement retroactively changing the wave function than there would be in affecting the time propagation of an operator into the past. Retroactively altering the formal entities of quantum mechanics, namely the wave function and the operators, does not qualify as non-local or reverse causality, since in no case is the outcome of a past measurement altered by a present event.

The issues raised by ’t Hooft also come into play with the delayed-choice experiments proposed by J.A. Wheeler.[8] In one version, the decision to insert or remove a beam splitter at the output end of an interferometer affects whether or not photons will behave as though there were interference from the other possible path. This is true even if the decision to insert or remove the splitter is made after the photon has entered the input end, and has presumably taken one or the other paths (if there is no output splitter) or followed both paths (if there is an output splitter). This has the bizarre implication that the choice of configuration event can effect the quantum state of something in the past of that choice. On its face, this would violate relativistic locality or even the principle of causality itself. Further, the ambiguity as to whether the photon follows one or both paths seems to be incompatible with a realist account of the photon.

Wheeler’s experiment was finally realized by Jacques et al. (2007) with sufficient safeguards to ensure that it was impossible for information from the choice-of-measurement event to reach the photon entering the interferometer.[9] Thus we apparently have an event that affects a space-like separated event, contrary to relativity.

We may invoke some of the conceptual tools employed by ’t Hooft in the context of Bell’s inequalities, and apply them to delayed-choice experiments, to offer an alternative account of the sense in which choice may alter the past. This requires us to reconsider the relationship between the quantum wave function and physical reality.

Lastly, we will examine the results of the BIG Bell Test Collaboration led by M.W. Mitchell (2018),[10] which ostensibly closed the freedom of choice loophole, though not in the sense demanded by ’t Hooft. Indeed, the collaborators admit that it is empirically impossible to refute superdeterminism, i.e., the supposition that all events, including human choices, are ultimately determined by anterior conditions. Nonetheless, allowing the reasonable assumption that the choices of measurement made by each of the crowd-sourced experimenters were not causally related to each other, this closes the loophole of previous Bell tests that made choices based on random quantum events, which might conceivably be causally correlated on a deeper level. Contrary to media reports, the BIG Bell Test did not prove free will but assumed it, though the results did show that the assumption of free will is consistent with quantum mechanical predictions for Bell tests. As the authors remark, following Bell, we need only assume that a human choice is free in the mathematical sense of a free variable, i.e., any value can be assigned to it, since it is not bound by any parameter or variable that conditions or predicts the measurement outcomes in question.

These latest experiments merit further consideration of whether a lack of statistical correlation proves a lack of causation between sets of events, and if so, in what sense causation is absent. Such analysis may require us to reconsider critically the physicist’s shorthand of making events the subjects of causation. We must always keep in mind clear distinctions among concepts such as determinism, causality, and reality, in order not to overvalue the implications of a particular finding.

1. Quantum Mechanical States and Measurements

In classical mechanics, we may define the physical state of a particle in terms of the quantitative values it has for certain physical properties, such as position, momentum, and charge. In quantum mechanics, however, the value of a physical property cannot be definitely fixed until a measurement is taken, via some sort of physical interaction (e.g., with a particle detector, a polarizing filter, or a magnetic field gradient), the outcome of which gives a specific value of the property being measured. Strangely, a set of identically prepared particles may yield different outcomes when measured by the exact same interaction conditions, though the statistical distribution of outcomes is predicted by the mathematical formalism of quantum mechanics.

Quantum mechanical formalism represents the physical state prior to measurement as a function ψ(x), where x denotes one or more independent variables x₁, x₂, x₃…. These variables could be the components of spatial position (x, y, z) or linear momentum (p_x, p_y, p_z), for example. If we know ψ(x) for time t = 0, we can determine what it will be for all future times, using the time-dependent Schrödinger equation, which has a form similar to the classical wave equation. Due to this resemblance and consequent wave-like behavior, the state function ψ(x) is commonly called the wave function.

There may be many different possible wave functions, corresponding to possible states of the system, which we may denote ψ₁(x), ψ₂(x), etc. We may make linear combinations of these functions to denote other possible states: r₁ψ₁ + r₂ψ₂ +… where the coefficients r₁, r₂, etc. can be any complex number. All possible linear combinations may be treated as points in an abstract state space of the physical system.

A state space has the mathematical properties of a vector space, which allows us to impose a convenient geometric interpretation of wave functions. The state space is defined as the set of all possible linear combinations of system states ψ₁, ψ₂, ψ₃… ψ_n (where n may be finite or infinite) and the inner product defining the geometric relationship between elements: <ψ_a, ψ_b> = ∫ψ*_a(x)ψ_b(x)dx, where ψ* denotes the complex conjugate of ψ, replacing the imaginary quantity i with -i wherever it appears in the function. This inner product lets us define the norm or length (i.e., distance from origin) of each vector ψ_a as the square root of ∫ψ*_a(x)ψ_a(x)dx.

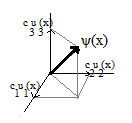
It is always possible to express a wave function ψ as a linear combination of orthogonal functions:

ψ(x) = c₁u₁(x) + c₂u₂(x) + c₃u₃(x) + … + c_nu_n(x)

The functions u_i(x) are said to be orthonormal, i.e., mutually perpendicular (orthogonal) and of unit length (normal) if represented as vectors in a vector space. The inner product of these functions ∫u*_i(x)u_j(x)dx equals 1 if i = j, which is to say the norm of each of these vectors is 1, and the inner product is 0 if i ≠ j, which is to say they are all orthogonal to each other in the state space. Such a set of functions forms an orthonormal basis, i.e., a set of perpendicular coordinate vectors for the vector space. Such a basis must contain n vectors, where n is the number of dimensions of the state space.

There are many possible sets of coordinate vectors for a given space, since one may orient the set of coordinate axes at different angles. In quantum mechanics, we are especially concerned with a particular kind of basis: one consisting of eigenfunctions.

A physical system is defined not only by a state or wave function but also by an observable property that can be measured. The observable is represented as an operator A that maps a function A(ψ) onto each wave function ψ. Since ψ is a function of the variables x = x₁, x₂, etc., A(ψ) will also be a function of these same variables, and thus will also be representable as a vector in the same state space. Thus A(ψ) is also a possible state of the system.

We are interested in cases where A(ψ) = aψ, where a is a real number. In such cases, ψ is geometrically colinear with A(ψ). Given that the operator A is Hermitian (as is always the case in quantum mechanics), it is algebraically provable that every wavefunction ψ(x) can be expressed as linear combination of these special cases.

ψ(x) = c₁φ₁(x) + c₂φ₂(x) + c₃φ₃(x) + …

where A(φ_i(x)) = a_iφ_i(x) [i = 1, 2, 3…]

The φ_i are special kinds of state functions called eigenfunctions or eigenstates. The real numbers a_i are called eigenvalues. The coefficients c_i can be any complex number, but their squared magnitudes are real, and have the following significance.

P(a_i) α |c_i|²

The probability of the eigenvalue a_i being measured for the observable physical property A is proportionate to the square of the coefficient c_i of the eigenstate φ_i(x) corresponding to that eigenvalue. Sometimes, more than one non-colinear eigenstate may have the same eigenvalue, in which case we must take the sum of the squared coefficients for mutually orthogonal eigenstates in this subspace to get the total probability for that value.

It is often (but not always) possible to normalize ψ(x), multiplying it by a constant (without loss of generality, since colinear vectors represent the same state) so that its squared norm ∫ψ*(x)ψ(x)dx = 1. If the eigenfunctions are also normalized to unit length in the vector space (again without loss of generality), then the sum of squared coefficients must likewise equal 1 in order for the sum Σc_iφ_i to give a total norm of 1. Now that the probabilities add up to 1, we can say that the squared coefficients are simply equal to the probability.

P(a_i) = |c_i|²

The wave function ψ(x), when normalized and expressed as a linear combination of normalized eigenfunctions, gives us the probability of each of the various possible outcomes of a physical measurement, the outcome of which always gives some definite real number, namely the eigenvalue. Any particular measurement, i.e., a single data point, will always yield an eigenvalue as the result, but we have no way of knowing which eigenvalue we will get except probabilistically. The wave function’s variables x = x₁, x₂, x₃… can give us no more than probabilistic knowledge.

Not all states can be represented as functions of variables. Some, like spin states, do not relate to any continuous variable. To accommodate such cases, we may replace the function ψ(x) with the vector |ψ⟩ (using Dirac notation), which may be represented as a column vector. The inner product of two states ψ_a and ψ_b is defined as ⟨ψ_a|ψ_b⟩, where ⟨ψ_a| is a row vector composed of complex conjugates of the components of |ψ_a⟩. This row vector is left-multiplied to the column vector |ψ_b⟩ in the usual way, taking the sum of the products of the corresponding components.

The operator A can be represented as a matrix that is left-multiplied to the state vector |ψ>. The quantum state can be represented in terms of eigenvectors:

|ψ⟩ = c₁|φ₁⟩ + c₂|φ₂⟩ + c₃|φ₃⟩ + …

where A|φ_i⟩ = a_i|φ_i⟩ [i = 1, 2, 3…]

The values of properties such as A are given only probabilistically, so we can only arrive at knowledge of the quantum state ψ of a particle by making repeated measurements of identically prepared particles with similar interaction conditions at the point of measurement or detection. A quantum measurement in this sense really consists of many repeated measurements and a statistical tabulation of outcomes. From this we infer knowledge of the prior quantum state, which is not so much the state of this or that particle, but of a one-particle system whose structure is gleaned from measuring an ensemble of particles prepared identically and subjected to the same interaction conditions, all at once or one at a time. Note that the system cannot be defined without reference to some measurement interaction, since that interaction helps define the structure of possible outcomes and their relative likelihood.

Since the classical notion of a particle involves being localized at some point in space, and spatial position in quantum mechanics is just another physical property that can only be known probabilistically, it is common among physicists to consider that classical particles are occurrent only as measurement outcomes, while the deeper physical reality is that indicated by the state vector or wave function, which in general is a mathematical composition or superposition of different possible outcomes. This deeper structure is the real electron or photon, etc., and we call them particles only equivocally, in reference to their particular manifestations after measurement interactions.

2. Two-Particle Systems and State Spaces

Although, in practice, each quantum measurement requires us to make repeated detections of many identically prepared particles, we consider something to be a one-particle system if the state space described by the measurement only covers the possible states of a single particle. For example, in a single-particle 1/2-spin system, the only possible values for z-spin are +ℏ/2, -ℏ/2. Suppose, however, we wanted to consider the possible states for a system of two particles. As long as the spin state of one particle is independent of the spin state of the second, we can define the two-particle system in a fairly uncomplicated way.

Let system I and system II be two one-particle systems, where some operator R is an observable in system I and operator S is an observable in system II. In our example, we are measuring the same property, z-spin, in both systems, but we nonetheless label the operators distinctly, since they are applied in distinct state spaces, those of systems I and II respectively. (Similarly, recall from algebra that a function is defined in part by its domain.) When there is no interdependence of states between systems I and II, i.e., they are non-interacting, then we can trivially augment the operators R and S so that they work in the other system’s state space, by making them act as the identity relation in the dimensions of the other state space. This is just a formal way of saying that measuring spin in system I does not affect spin measurements in system II and vice versa.

We may label these augmented operators R' and S'. They each can be applied in the combined state space of what is now a two-particle system. The two operators commute with each other, meaning that the order in which they are applied does not matter: R'S' = S'R'. The state space of the combined system I+II will be a tensor product of the state spaces of systems I and II. If the state space of system I has m dimensions and that of system II has n, the state space of the two-particle system will have m × n dimensions. The number of dimensions equals the number of linearly independent eigenstates, so if system I and system II each have two such eigenstates, as in our example, then the two-particle system will have 2 × 2 = 4 eigenstates. The commutativity of R' and S' allows us to define unambiguously a total spin operator that simply adds the spins of each particle to give the total spin of the two-particle system.

Similarly, the state or wave function in the two-particle system will be an outer product of the wave functions of system I and system II. It will have mn components, where a state in system I had m vector components and a state in system II had n vector components. In our example, this will be four components. Strictly speaking, this outer product is no longer a vector, and should be represented in Dirac notation as |ψ_I⟩ ⊗ |ψ_II⟩, but it is common practice to use a shorthand such as: |ψ_I; ψ_II⟩.

Although |ψ_I⟩ ⊗ |ψ_II⟩ is not a vector, the tensor product of spaces is still a true vector space. Its elements are the vectors |ψ_I⟩ and |ψ_II⟩, which form the combined vector space by a bilinear map (or a multilinear map for systems of more than two particles).

This may seem to be a mathematically excessive way of dealing with the relatively simple problems of adding property values across particles and multiplying the number of possible states. These problems are simple, however, only when there is no interdependence of states between systems and the relevant operators commute. When there is such interdependence, we can no longer afford to be naïve about the distinctions among state spaces and their respective operators.

3. Entangled States

Certain physical processes create pairs of particles whose quantum states are distinct, yet interdependent, so we call them entangled states. For example, a spin-zero particle may decay into two spin-1/2 particles, which must have opposite spins, since, by the law of conservation of angular momentum, their total spin must be zero. We can measure the spin of a particle by seeing which way it deflects (up or down) under a magnetic field gradient (i.e., a magnetic field that increases linearly in strength along a certain direction). Suppose we apply a magnetic field with a gradient in the direction of the z-axis. If we measure one of the particles to be z-spin up, then we know the other must certainly be z-spin down, by conservation of angular momentum, even though we have yet made no attempt to measure the other photon directly.

This seems to have perplexing implications regarding the interpretation of quantum mechanical states prior to measurement. Was the other particle definitely spin-down even before we measured the first photon, or did it become so when we made the measurement? If the latter, this would run into problems with relativity, since we cannot define simultaneity unambiguously for two distinct points in space. If the former, consider that we could have chosen instead to measure the first particle’s spin with respect to the x-axis, in which case, by quantum formalism (and confirmed by experiment), there is a 50% chance the second particle would be z-spin up (since the x- and z-spin operators do not commute). That would mean that prior physical reality was somehow determined by our choice of measurement!

Mathematically, entanglement implies that we cannot describe the two-particle system by simply augmenting each one-particle system’s operator to act as an identity operator in the other system. Since each operator non-trivially affects the other state space, it is not possible to express the two-particle system’s state in terms of a state vector for each one-particle system. The states of the two particles are truly entangled.

The Einstein-Podolsky-Rosen (EPR) paradox and Bell’s inequalities deal with the problems raised by entangled states, where we cannot treat the quantum state of one particle as independent of that of another particle. Problems include: (1) whether physical properties have definite values prior to measurement; (2) whether measurement of one particle can alter the quantum state of another, in apparent violation of the relativistic principle of locality; and (3) whether our choice of which property to measure in one particle can retroactively alter the state of another. These last two issues may require us to challenge the notion that the so-called quantum state or wavefunction corresponds to a physically real entity. Rather, there may be no such thing as a quantum state or wavefunction in itself, but instead the physical reality is indicated by the complex of wavefunction and observable combined. Thus it may be impossible to define the physical state of a system independently of the settings of a measurement apparatus, since the system necessarily includes the apparatus, interaction with which causes the realization of a definite value of the measured property.

4. Einstein, Podolsky and Rosen’s Argument

In a famous 1935 paper, Albert Einstein and his postdoctoral trainees Boris Podolsky and Nathan Rosen[11] argued that the paradoxes of measurements on interacting systems (which we now call entangled states) disproved the claim that quantum mechanics is a complete theory, accounting for every element of reality that determines the values of physical properties. Rather, the wave function gives only a partial account, yielding probabilistic knowledge, while the full account must be complemented by some unknown variables that resolve the paradoxes. Such an account could conceivably restore strong determinism in physics. We will examine the paper’s argument and its assumptions in some detail.

4.1 Realist Definition of Physical Theory

According to the authors, whom we will henceforth call EPR, the concepts of a physical theory are intended to correspond with the objective reality, which is independent of any theory. Here a physical theory is understood to mean a system of concepts that is intended to tell us something about a physical reality that would exist even if there were no humans to develop such concepts.[12]

This definition entails three realist suppositions: (1) the existence of an objective reality; (2) the possibility of making this reality known via conceptual theories that refer to it; (3) the independence of reality from any particular theory. The first two suppositions are absolutely indispensable to the scientific method. Without them, scientists would have nothing to do. The third supposition might be seen as implying an anti-idealist view of concepts, regarding them as purely human inventions. This philosophical position is not essential to science, and it is conceivable that objective reality at some deeper level depends on ideal concepts, abstracted from their instantiation in a human thought. If we are to accommodate this possibility, we should simply say that objective reality is independent of human mental activity developing a theory, at least insofar as the determinate human mental activity itself is not the subject of that theory.

4.2 Completeness of a Theoretical Description

The first question raised is whether quantum mechanical formalism is truly a physical theory as defined above. Surely, we intend for it to correspond to physical reality in some way, as we expect it to predict the outcomes of experiments at least probabilistically. Yet it is less certain that each of its variables, operators and states is really intended to correspond to something physically existent, or whether these are merely formal constructs that help us make predictions about outcomes determined by unknown physical objects or properties.

EPR make this distinction by evaluating a physical theory under two criteria: (1) Is the theory correct? and (2) Is the description given by the theory complete? Correctness is determined by the theory’s agreement with human experience, i.e. with experimental results. This is an empiricist criterion, a presupposition of scientific method. Yet EPR consider that we must also give an affirmative answer to the second question for the concepts of the theory to be satisfactory. Mere prediction of outcomes is not enough; EPR demand that a physical theory must also include concepts that give us a picture that represents or describes physical reality.

If the concepts do not have physical realities as their referents, then what we really have is a purely mathematical calculating device, not a physical theory that explains how reality works. It would be akin to the various devices for calculating celestial motions under a geocentric paradigm. At first, it was believed that Copernicanism was another such device, not an account of physical reality. Our recognition that it is in fact the latter shows that this is a meaningful distinction, and we expect more of our theories than merely successful computation.

It is notoriously difficult, however, to prove that a computationally accurate theory also consists of concepts that correspond to physical entities. Copernicanism is an excellent example, for it was accepted immediately as a mathematical tool, but centuries passed before it was accepted by all of Europe as a truly physical theory, and direct experimental confirmation of the diurnal rotation of the Earth was not made until the nineteenth century. In principle, one could always insist that a computationally accurate theory is not physically descriptive in its concepts. At some point, however, parsimony argues in favor of the theory, if it uses the minimal number of variables necessary to account for the phenomenon. Still, there remain difficult cases. We cannot prove to this day, for example, that electric fields are real entities, rather than mere formalisms for calculating the interaction strength between source particles. In practice, physicists treat them as though they were physically real, but they would get the same results on the opposite assumption.

In the case of quantum mechanics, it is controversial, even among those who hold the conventional Copenhagen interpretations, exactly what kind of physical reality, if any, should be attributed to variables, operators and states. Operators represent physical observables, i.e., physical properties that we can observe, and always as having one of the eigenvalues of the operator as its observed value. The operators, applied to wavefunctions, predict the statistical distribution of outcomes of repeated observations under like conditions, so it would seem they tell us something about the physical properties observed. Does it follow, however, that the operator corresponds to a physical property, even in its description of the time evolution of probabilities between observations? Likewise with the state or wavefunction: Does it really correspond to a physical state of some extramental object, or is it just a description of the imperfect knowledge of any observer? These are not the only possibilities. Whatever we think of the wavefunction, this will affect our interpretation of operators, which are definable only with respect to wavefunctions.

EPR recognize the difficulty of defining completeness. After all, even our truly physical theories may give only an imperfect or approximate description or representation of physical reality. It would seem that a complete theory must include all the physical properties that determine the phenomenon in question, to the degree of accuracy to which we wish to understand it. The limitation on accuracy allows us to ignore friction and other factors that may affect the phenomenon incidentally, without derogation of our complete understanding of the phenomenon itself.

They offer the following as a necessary condition of completeness: every element of the physical reality must have a counterpart in the physical theory. This raises the question of what counts as an element. Presumably, a theory for a given phenomenon need not account for all incidentals, but only for those factors that contribute to outcomes. EPR wished to avoid having to invoke a priori metaphysical elements, i.e., hidden causes that do not change predicted outcomes but are nonetheless metaphysically necessary. To confine their scope to empiricism, they offer this sufficient condition of an element’s reality:

If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.

As EPR admit, this is a sufficient but not necessary condition of reality. While this premise has been identified by subsequent commentators as realism, in fact it is something narrower, a particular kind of realism where we can predict values with certainty, i.e., strong determinism. The claim is that any physical quantity whose value can be predicted with certainty must correspond to some element of physical reality. That is to say, quantitative predictability is sufficient evidence of reality. The authors restrict predictability to full deterministic certainty, since this sort of predictability is unequivocally real.

The authors nowhere disprove that a merely statistical predictability might also be evidence of reality. Quantum mechanics may not be able to predict a value, but it can accurately predict the distribution of values for many instances of an observation. Their argument is not that the imperfect predictability of values in quantum mechanics is evidence of unreality. They are simply taking a cautious, restrictive criterion for reality, in order to show that, even if an unquestionably sufficient condition is met, a contradiction will result.

4.3 Incompleteness Dilemma

In quantum mechanics, a physical state is supposed to be completely characterized by the wave function ψ(x). An operator A can be applied to ψ, representing the act of measuring some physical property A. This gives us the probabilities of observing each of the possible values of that property as a measurement outcome. We recall that ψ(x) can be expressed as a sum of eigenfunctions φ_i(x) such that A(φ_i(x)) = a_iφ_i(x), where a_i is a real number known as the eigenvalue. The eigenvalues are the possible values that can be observed for that property.

Eigenfunctions may be represented geometrically as vectors forming an orthogonal coordinate basis for the abstract space spanning all possible states under that operator, i.e., all possible quantum states with respect to the property represented by the operator. Thus absolutely any wavefunction ψ, being representable as a vector in that same space, is expressible as a linear combination of eigenfunctions:

ψ(x) = c₁φ₁(x) + c₂φ₂(x) + c₃φ₃(x) … + c_nφ_n(x)

The squared magnitude of each coefficient c_i gives the probability that the measured value will be the eigenvalue a_i. (This assumes that we have normalized ψ and all φ_i.) In the special case where ψ(x) = φ_i(x), i.e. where ψ(x) is an eigenfunction of the operator A, we know with certainty that the observed value will be the eigenvalue a_i corresponding to that eigenfunction.

However, when ψ(x) is not an eigenfunction of the operator, we can no longer speak of the physical property A having a particular value. We cannot predict the value of A that something in such a state ψ will have, except in terms of probabilities. We must take a measurement of the particle in order to obtain a definite value. Yet the act of measurement (in the conventional interpretation of wavefunction collapse) disturbs the particle, altering its state, so it is no longer in ψ but in some eigenstate φ_i.

In the case of non-commuting operators, where AB ≠ BA, precise knowledge of one observable mathematically precludes precise knowledge of the other. This is because any wavefunction that is an eigenstate of A will not be an eigenstate of B, and vice versa. In conventional interpretations of quantum mechanics, this uncertainty in the value of one or the other property is not considered a mere lack of knowledge, but an absence of physical reality. That is to say, the physical property B has no definite value when A is measured, and there is no physically real definite value of A when B is measured.

EPR are largely correct in their characterization of conventional interpreters as denying that properties have any definite real values between measurements. However, just because conventional interpreters deny both the full predictability and continuous reality of property values, it does not follow that uncertain predictability implies lack of reality. Full predictability is only a sufficient, not necessary, condition of reality.

In contrast with conventional interpreters, EPR confine their claims about non-commuting operators to the following. First, precise knowledge of one observable precludes precise knowledge of the other. This is a statement about what the theory can do, not about physical reality. Second, any attempt to determine the latter experimentally will alter the state of the system in such a way as to destroy the knowledge of the first. Here we have a hybrid statement: measurement is altering physical reality, assuming the quantum state corresponds to such reality, and it destroys knowledge, i.e., affects what the theory is able to do. It remains to be seen whether the quantum state really does correspond to physical reality, and EPR will examine how this assumption may break down.

From the two preceding claims, which are generally accepted by quantum theorists, EPR infer:

Either (1) the quantum-mechanical description of reality given by the wave function is not complete or (2) when the operators corresponding to two physical quantities do not commute the two quantities cannot have simultaneous reality.

They justify this inference as follows:

For if both of them had simultaneous reality—and thus definite values—these values would enter into the complete description, according to the condition of completeness. If then the wave function provided such a complete description of reality, it would contain these values; these would then be predictable. This not being the case, we are left with the alternatives stated.

Here the reality of a physical property is assumed to entail having a definite value. This is true insofar as we regard properties as existents, though it is conceivable that they should have other modes of being, such as potentiality or propensity, which would not require realization of a definite value. Note that having a definite value, per se, does not entail strong determinism, i.e., the full predictability of that value. Nonetheless, a theory that pretends to be complete should be able to give an account of all the definite values held by the properties it pretends to describe, assuming that such definite values exist. If the theory contains these values, the authors say, then these values are predictable, i.e., they can be generated by the theory.

Is this last inference certain? After all, it is conceivable for a physical variable to have definite values at every point in time, yet not have predictable values. For example, perhaps something oscillates erratically between spin up and spin down, so there is no way of predicting when it will change values next, though it will always have a definite value. If the entire sequence of values were contained in a theory, we should say they are predictable, but they might be contained only in a probabilistic sense, say, if the theory gives the probability of the spin changing values based on the time elapsed since the last change. Thus we would have a theory that does give an account of the definite values of a property without making these values predictable.

In the special case of spatial position considered as a property, definiteness is indeed closely tied to predictability, if we make the further assumption of continuity of trajectory. With that assumption, any knowledge of position at a given point in time greatly limits the range of possible positions in the immediate future, making it predictable to a high degree of accuracy in the short term. Even on this assumption, however, it is conceivable that the direction of motion could vary continuously by some random factor, making the long-term trajectory unpredictable. So once again reality and predictability are distinct conditions.

By requiring a complete theory to predict all definite values of real properties, EPR have incorporated strong determinism into their notion of realism, notwithstanding their earlier admission that full predictability is merely a sufficient condition of reality. To avoid this error, we should instead admit only the converse: if a theory predicts all definite values, then it is complete.

Quantum mechanics purportedly gives a complete description of a system’s physical reality, which seems reasonable, for the information obtainable from a wave function seems to correspond exactly to what can be measured without altering the state of the system. We shall show, however, that this assumption, together with the criterion of reality given above, leads to a contradiction.

The criterion of reality is presumably what we quoted earlier:

If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.

To make this a criterion of reality is to mistake a sufficient condition, namely predictability, for a necessary condition. So the following thought experiment proposed by EPR (revised for clarity to non-physicists) really deals with predictability rather than reality as such.

4.4 Generalized Problem of Entanglement

Suppose we have two systems, I and II, and let the symbol x_I represent all the variables x₁, x₂, x₃… characterizing system I, while x_II represents the variables y₁, y₂, y₃… characterizing system II. Further suppose that each system is initially in a state characterized by the wavefunctions ψ_I(x_I) and ψ_II(x_II) respectively.

Recall that these wavefunctions help us predict the probability that a physical property will have a certain value if measured. For system I, for example, the physical property A can have possible values a₁, a₂, a₃, etc. The wavefunction ψ_I is always representable as a linear sum of eigenfunctions of A, i.e., functions u_i(x_I) such that A(u_i(x_I)) = a_iu_i(x_I), where the eigenvalues a_i are the possible values of measurements of A. Thus we can write:

ψ_I(x_I) = c₁u₁(x_I) + c₂u₂(x_I) + c₃u₃(x_I) + …

The squared magnitude of each coefficient c_i gives the probability that the value of the physical variable A will be the eigenvalue a_i corresponding to the eigenfunction u_i(x_I), if A were to be measured at this time.

We might choose to measure some other physical property B in system I, which has eigenvalues b₁, b₂, b₃… associated with eigenfunctions v₁(x_I), v₂(x_I), v₃(x_I)… The wavefunction ψ_I may then be written as:

ψ_I(x_I) = d₁v₁(x_I) + d₂v₂(x_I) + d₃v₃(x_I) + …

The coefficients d_i need not be the same as the c_i in the previous formula.

If the same properties A and B were also observables in system II, we could produce similar formulas for ψ_II(x_II), but we would now operating in a different state space, that defined by the variables x_II = y₁, y₂, y₃, etc. Thus the eigenvalues, eigenfunctions and coefficients could be altogether dissimilar to those in system I.

Suppose the state of system I is defined by n variables, so that x_I = x₁, x₂, x₃… x_n. The abstract state space for system I thus has n dimensions, and there can be no more than n distinct eigenvalues, each corresponding to a linearly independent (i.e., non-colinear) eigenstate, for any observable (e.g. A or B) that can be measured in that system. Note that the same variables may define eigenfunctions (eigenstates) for different observables. The question of completeness is whether there might not be some other variables that help determine the values of observable properties, or if the variables x_I are the only variables that have any predictive power for the values of observables in system I. Only in the latter case is the quantum formalism complete.

Similarly, the state of system II may be defined by m variables, so x_II = y₁, y₂, y₃… y_m, where m need not be equal to n. Thus the state space for system II will have m dimensions, while that of system I has n dimensions.

The variables x_i or y_i, in general, need not neatly correspond one-to-one to a particular physical property (A or B) or its values (the eigenvalues a_i or b_i, with associated eigenstates). Naturally, the variables x_i or y_i must be individually or collectively correlated to at least one observable property, or we would have no cause for suspecting the existence of these variables in the first place.

The spatial wavefunction ψ(x), where x is spatial position along the x coordinate, is a special case where the wavefunction variable does indeed correspond to an observable property. The values of the wavefunction’s variable x correspond to the possible values of the physical property of spatial position defined by the operator X. This is not the case for the variables of other kinds of wavefunctions, however. In general, a variable x_i characterizing the quantum state (distinguishing it from other possible states of that system) is not identical with the continuous real variable defining the range of values that can be held by a physical property. In quantum mechanics, most physical observables do not even have a continuum of possible values, but only the discretely separated eigenvalues permitted by the operator for that observable.

4.5 Post-Interaction Measurement of Entangled States

In the entangled states problem presented by EPR, we suppose that systems I and II, initially in the states ψ_I and ψ_II, are allowed to interact starting at some time t = 0 and ending at some later time t = T. It is simplest to think of system I and system II each representing a distinct particle, though we must be wary of bringing in classical assumptions about particles as corpuscular entities with absolute existence as substances, when instead a particle may be merely a particular manifestation or state of the deeper physical reality indicated by the wavefunction.

Due to the interaction of the two systems, we can henceforth predict the probabilities of measurement outcomes only in terms of a combined wavefunction Ψ(x_I, x_II) for the combined system I+II. This combined wavefunction would be in a state space that is the tensor product of the state spaces of systems I and II. The state space of I+II will have mn dimensions, where the state space of system I has m dimensions and that of system II has n dimensions. EPR tacitly assume that the dimensions of state spaces I and II are countably infinite, without loss of generality, since we could always suppose that Ψ has components of zero in some dimensions. The state space of I+II will likewise have a countably infinite number of dimensions. We assumed from the outset that the variables x_I are independent of the variables x_II, i.e., that the state spaces of I and II are not overlapping (e.g., if they describe properties of two distinguishable particles), so we can express the combined wavefunction Ψ as follows:

Ψ(x_I, x_II) = ξ₁(x_II)u₁(x_I) + ξ₂(x_II)u₂(x_I) + ξ₃(x_II)u₃(x_I) + …

Here Ψ is expressed as a linear combination of eigenfunctions u_i of the property A (in the state space of system I), whose coefficients are wavefunctions ξ_i of the variables x_II of system II (in the state space of system II). Note that the wavefunctions ξ_i(x_II) are not necessarily eigenfunctions of any observable in the state space of system II. Also, we could just as well have chosen to represent Ψ as a linear sum of eigenfunctions of some observable in system II, with coefficients ω_i (distinct from ξ_i) that are wavefunctions of the system I variables x_I, but then these wavefunctions ω_i(x_I) would not necessarily be eigenfunctions of any observable in system I.

The time-dependent Schrödinger equation allows us to calculate Ψ even for times t > T, after the interaction of systems I and II has ceased. Nonetheless, the two systems remain characterized by the joint wavefunction Ψ, even if they somehow become remotely separated in physical space or are otherwise non-interacting. In general, the states may be entangled in such a way that it is mathematically impossible to distinguish the contributions of the two systems. The only way we can once again identify distinct states for each system, I and II, is by taking a measurement of an observable of one or the other system, a procedure known as reduction of the wave packet.

Let a₁, a₂, a₃ … be the eigenvalues of physical property A corresponding to eigenfunctions u₁, u₂, u₃… of system I. Suppose we take a measurement of property A in system I at some time t_m > T, and get a value of a_k. Then the wavefunction of system I+II becomes Ψ(x₁, x₂) = ξ_k(x_II)u_k(x_I). All other possibilities are zero, so system I+II is in this reduced or partly collapsed state.

It is algebraically equivalent to represent Ψ as a sum of eigenfunctions v_i of some other system I observable B:

Ψ(x_I, x_II) = φ₁(x_II)v₁(x_I) + φ₂(x_II)v₂(x_I) + φ₃(x_II)v₃(x_I) + …

Here the coefficient wavefunctions φ_i(x_II) are not, in general, eigenfunctions of any observable in the state space of system II.

Let b₁, b₂, b₃ … be the eigenvalues of physical property B corresponding to eigenfunctions v₁, v₂, v₃… in system I. Suppose, instead of measuring A, we measure property B in system I at t_m > T, and get the value b_r. Then the wavefunction of system I+II becomes Ψ(x₁, x₂) = φ_r(x_II)v_r(x_I).

In short, the joint wave function Ψ at measurement time t_m > T can have one of two forms, depending on whether we choose to measure property A or B in system I.

Ψ(x₁, x₂) = ξ_k(x_II)u_k(x_I) if A is measured in system I.

Ψ(x₁, x₂) = φ_r(x_II)v_r(x_I) if B is measured in system I.

Operating on the stipulation that the two systems are no longer interacting, EPR treat systems I and II as though they have separate existence after T. Thus ξ_k(x_II) may be considered the wavefunction of system II when A is measured to be a_k in system I, and φ_k(x_II) is the wavefunction of system II when B is measured to be b_k in system I. Since systems I and II are no longer interacting, nothing that is done to one system can affect the other, for that is what it means not to interact. Thus measuring A or B in system I should not physically affect system II.

In apparent contradiction with this expectation, we get different wavefunctions for system II depending on whether we measure A or B in system I after the two systems have ceased interacting. EPR correctly remark that there are actual cases where the system II wave functions ξ_k and φ_r are eigenfunctions of non-commuting operators, which we may call P and Q respectively. It is algebraically impossible for an eigenfunction of P to be an eigenfunction of Q and vice versa. Thus if we measure A in system I, then system II will be in an eigenstate of P but not of Q. If we were to measure B in system I, then system II would instead be in an eigenstate of Q but not of P.

Suppose we have such a case, i.e., where ξ_k is an eigenfunction of P in the state space of system II with eigenvalue p_k, while φ_r is an eigenfunction of Q in the state space of system II with eigenvalue q_r. Thus if we measure A in system I, we can predict with certainty, and without in any way disturbing the second system, the value of P in system II, and if we measure B we can likewise predict with certainty the value of Q. In short, the state of system II is:

ξ_k(x_II), an eigenstate of P but not of Q, if A is measured in system I.

φ_r(x_II), an eigenstate of Q but not of P, if B is measured in system I.

Recall earlier that it was an established criterion of reality, i.e., a sufficient condition of reality, that a fully predictable quantity is also real. When something is in an eigenstate of an observable, its value for that property becomes fully predictable. Thus the full predictability of the value of P when A is measured implies that the property P is an element of reality, and likewise the full predictability of Q when B is measured implies that the property Q is an element of reality. But, as we have seen, both wave functions [ξ_k and φ_r] belong to the same reality.

The last quoted statement depends on the inference that no measurement done on the first system can physically affect the second system, since, by assumption, the two systems are no longer interacting. This implies that ξ_k and φ_r both describe the same reality of system II after interaction has ceased.

EPR infer from non-interaction after T that we may again speak of system I and system II as independent existents, at least once a measurement has been made. Thus they interpret the coefficient wave function ξ_k(x_II) as being the wave function of system II, even though it is still just a factor in the joint wavefunction Ψ. Yet, as EPR themselves admit, it is impossible to calculate the state for either system I or II at any time after T prior to reduction of the wave packet by making a measurement. Thus we must keep in mind that we are only justified in treating systems I and II as having distinctly identifiable states after a measurement. Prior to that, we may speak only of the state of the combined system I+II, which may have interaction terms between the state spaces of I and II, even after the period of interaction has ceased. This is what is meant by entanglement.

That being said, if quantum mechanics gives a complete account of physical reality, it should include all elements of reality, namely the value p_k of P for system II in the state ξ_k if A is measured, and the value q_k of Q for system II in the state φ_k if B is measured. The apparent supposition by EPR that both of these observables (P and Q) should be considered elements of reality, even though we can in fact only measure only A or B, not both, seems to be informed by the supposition that measurement of one system cannot change the physical reality of the other, without violating the non-interaction assumption.

…since at the time of measurement the two systems no longer interact, no real change can take place in the second system in consequence of anything that may be done to the first system. [Emphases added]

The emphasized text draws attention to some assumptions made in this inference. First, what is meant by a real change? Obviously, a change in the value of a physical property would constitute a real change. It is less obvious that changing the wavefunction constitutes a real change, and perhaps that is what is being called into question.

The absence of interaction is by assumption. Recall that this is a purely formalistic treatment, not based on an experimental result. It would remain for future researchers to design experiments meeting this condition. One apparent way to guarantee non-interaction would be to have the systems be two entangled particles that move far away from each other, so they could not possibly interact, even with light-speed signaling. This requires us to assume locality, i.e., that physical changes can be effected only in the immediate vicinity of an agent. Under relativity, this implies that physical effects must be propagated by signals travelling less than or equal to the speed of light. The assumption that physical causation is confined by locality is implied in the expressions time of measurement and in consequence. If a change in one system is to effect a change in the second, the latter change must take place after the first change (which occurs at the time of measurement).

Expressed relativistically, the change to the second system must be in the future light cone of the change to the first (ostensibly the event of measurement). The changes conceivably could occur simultaneously if the systems are in the same location, but not if they are any distance apart, by the principle of locality. Note that this assumes that it is meaningful to speak of the systems being in certain locations.

The authors, especially Einstein, considered it problematic that we can assign two different wave functions to the same reality. Yet the interpretation that ξ_k and φ_r refer to the same reality follows only if we assume that the reality of system II cannot be conditioned by our choice of what to measure in system I. This is exactly the paradox that would be explored in depth as a result of the EPR problem.

What EPR wished to challenge is the notion that the wavefunction really gives an account of physical reality, or at least a complete account of it. To accomplish this, they claimed to show a direct contradiction necessarily results if we assume that the wave function gives a complete account of physical reality.

4.6 Logical Structure of the Argument

EPR complete their proof as follows (paraphrased slightly):

First Premise (supposedly proven earlier): Either (1) the quantum-mechanical description of reality given by the wave function is not complete or (2) the two physical quantities corresponding to non-commuting operators cannot have simultaneous definite reality.

Second Premise: Assuming that (NOT 1) the wave function gives a complete description of physical reality, it followed that (NOT 2) two physical quantities with non-commuting operators can have simultaneous reality.

Conclusion: The quantum-mechanical description of physical reality given by wave functions is not complete.

The logic is straightforward:

Either (1) or (2).
If (NOT 1), then (NOT 2).
Therefore (1).

In conclusion, the quantum mechanical wave function is not a complete description of reality. Note that EPR are not claiming that there is simultaneous reality to the values of non-commuting observables. Rather, they use the apparent contrary finding as a basis for finding a contradiction with the supposition that the quantum mechanical description is complete.

Of course, the conclusion is no stronger than the premises. Recall that EPR made this a necessary condition of completeness for a theory:

Every element of the physical reality must have a counterpart in the physical theory.

What counts as an element of physical reality? We have this sufficient condition:

If a physical quantity can be predicted with certainty, then there is an element of physical reality corresponding to it.

If some quantity has a definite value that can be predicted with certainty, then it corresponds to an element of physical reality and must be included in a complete theory. Since this is only a sufficient condition, it is conceivable that unpredictable quantities might also be elements of reality, but we set those aside.

To prove the first premise, EPR argued that if non-commuting observables had simultaneous reality, and thus definite values, these values must be found in any complete theoretical description of physical reality. If the wave function contained these values, they would be predictable. This seems to rely on an implicit premise, which we may write as:

A complete theory must render all real values predictable.

This effectively makes full predictability or strong determinism a necessary condition of completeness for a theory. In fact, it suffices for completeness that every element of reality is in the theory, even if it is not thereby made fully predictable. As EPR admitted earlier, full predictability or determinism is only a sufficient condition of reality, not a necessary condition.

Thus the first premise remains unproven, and the conclusion does not follow, unless we make determinism rather than realism our postulate. This confusion has informed most subsequent responses to the EPR argument. The first premise entails not merely realism, but specifically a deterministic realism.

The second half of the second premise, as we have seen, relied on the principle of locality. The finding that the non-commuting observables P and Q have simultaneous reality depends on interpreting non-interaction as implying that measurement of one system cannot affect the physical state of its spatially separated counterpart. Without this assumption, it is unjustified to infer that the system II must have definite, fully predictable values for both P and Q, regardless of whether we choose to measure A or B in system I. It is only by assuming that measurement of one system cannot affect the other that EPR can infer that the definite values for P and Q in system II must have been held even prior to measurement of system I, or at any rate independently of that measurement.

Locality is a specific version of the broader principle of causality. Nonetheless, the relativistic account of space and time makes temporality and locality so closely interrelated that we could not conceive of non-local interactions without also allowing an agent to affect its own past (in at least some reference frames), rendering causality paradoxical and incoherent. Thus, under relativity, the principle of causality would seem to stand or fall with locality.

The EPR argument and its eventual refutation by actual experiment are frequently considered to be tests of realism, but in fact they are tests of the twin postulates of locality and determinism. It is not clear whether one or the other postulate has been refuted, much less that the more fundamental principles of causality and realism have been contradicted. To facilitate our discussion of responses and experimental findings, we should first clarify the meanings of these terms.

Continue to Part II

Notes

[1] X is spatially separated from Y means that the events X and Y are separated by a space-like interval in spacetime, i.e., an interval that cannot be traversed by any signal traveling at the speed of light or slower. Note that X and Y are not places in space, but events, so they have both space and time coordinates, and accordingly, spatially separated or space-like separated does not mean some distance apart in space, because the time component is also critical.

Per special relativity, there is no privileged coordinate system of space and time, so X could be before, after or simultaneous with Y, depending on choice of reference frame. (A frame of reference is determined by the relative velocity of an observer, not his location.) This ambiguity results in no temporal paradoxes, since it is impossible for a signal to travel between X and Y, so one event cannot be the cause or effect of the other in any frame.

Spatially or space-like separated events are contrasted with time-like separated events. If events W and Z are time-like separated, one is unambiguously in the past of the other, regardless of choice of reference frame. However, the temporal duration versus spatial distance between events will vary depending on choice of frame. All causally linked events are separated by time-like intervals, and the history or world line of any object will follow a time-like trajectory.

[2] Einstein, A., Podolsky, B., Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 47 (1935):777-780.

[3] Bell, J.S.. On the Einstein-Podolsky-Rosen Paradox. Physics 1 (1964):195-200.

[4] Sakurai, J.J.. Modern Quantum Mechanics. Reading, Mass.: Addison-Wesley, 1994. pp. 223-232.

[5] Bohm, D., Hiley, B.J. The Undivided Universe. London: Routledge, 1993. pp.293-294.

[6] Weihs, G., Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. Violation of Bell’s Inequality under Strict Einstein Locality Conditions. Phys. Rev. Lett. 81 (1998):5039-5043.

[7] ’t Hooft, G. On the Free-Will Postulate in Quantum Mechanics arXIiv:quant-ph/0701097v1 15 Jan 2007.

[8] Wheeler, J.A., in Quantum Theory and Measurement, J.A. Wheeler, W.H. Zurek, eds. Princeton, NJ: Princeton Univ. Press, 1984. pp. 182-213.

[9] Jacques, V., Wu, E., Grosshans, F., Treussart, F., Grangier, P., Aspect, A., Roch, J.-F. Experimental Realization of Wheeler’s Delayed-Choice Gedanken Experiment. Science 315 (2007):966-968.

[10] The BIG Bell Collaboration: Mitchell, M.W., Abellán, C., Tura, J. et al. Challenging local realism with human choices. Nature 557 (2018):212-216.

[11] Einstein, A., Podolsky, B., Rosen, N., op. cit. [Note 2]. Podolsky, a research fellow, wrote the final draft, which Einstein felt did not adequately emphasize the key issue. Rosen, a research assistant, had studied entangled states in great depth.

[12] For EPR, as for practically all scientists and philosophers before 1990, something is a scientific theory as long as it attempts to give a systematic conceptual explanation of observable facts, regardless of its degree of correctness or evidentiary support. Working hypotheses and speculations could be considered kinds of theories. (See, e.g., Webster’s Third New International Dictionary, 1981, or any text on science or philosophy of science from the period.)

A more restrictive definition of scientific theory, confining it to comprehensive theories that have a strong evidentiary basis, was adopted by the National Academy of Sciences in the 1990s for polemical use in the creationist controversies in the United States at the time. In practice, however, the development of theory frequently outpaces experimental confirmation, and speculative fields such as superstring theory are deservedly called theories even before they can be confirmed empirically. Conversely, theories meeting the restrictive definition do not thereby become unassailable, but remain no stronger than the evidence and arguments in their favor. We cannot change reality by changing the definitions of terms.

© 2019 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org